1 . Tam giác cân là gì? – Khái niệm tam giác cân
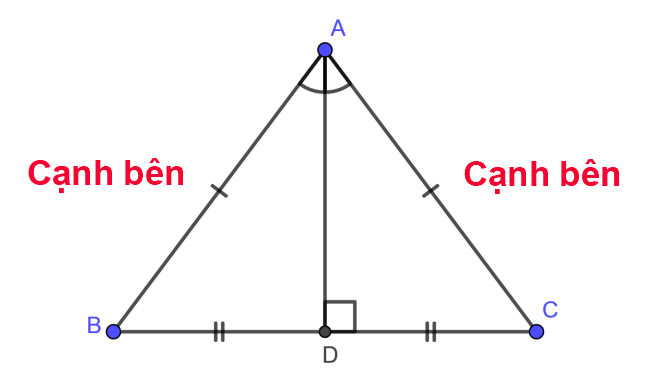
Tam giác ABC cân tại A.
AB, AC là các cạnh bên, BC là cạnh đáy.
Xét tam giác ABC, có AB = AC => Tam giác ABC cân tại A
2 . Tính chất tam giác cân
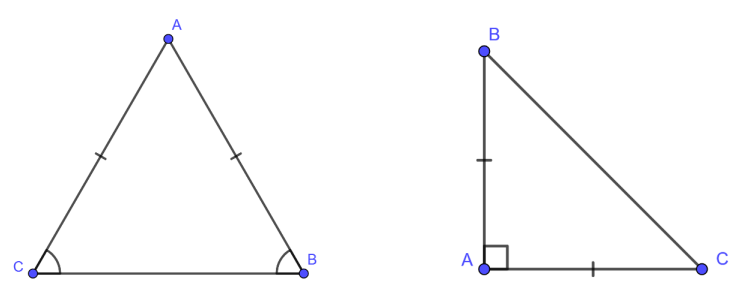
- Trong một tam giác cân hai góc ở đáy bằng nhau: Tam giác ABC cân tại A có hai góc ở đáy
- Nếu một tam giác có hai góc bằng nhau thì là tam giác cân. Vị dụ: Xét tam giác ABC có
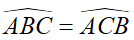thì tam giác ABC cân tại A. - Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau. Tam giác ABC vuông cân tại A có AB = AC và hai góc ở đáy
- Trong tam giác cân, đường trung tuyến ứng với cạnh đáy, đồng thời là đường cao, đường phân giác của tam giác đó.
Ví dụ: Tam giác ABC cân tại A, AD là đường trung tuyến ứng với cạnh đáy BC.
Suy ra, AD là đường cao và là đường phân giác của góc A
3 . Cách chứng minh tam giác cân
Có 2 cách chứng minh tam giác cân:
+ Cách 1: chứng minh tam giác đó có 2 cạnh bằng nhau
Δ ABC cân ở A có: cạnh AD chung, BD = CD
KL: AB = AC
Chứng minh:
Ta có: Cạnh AD chung
BD = CD
Góc ADB = Góc ADC
=>Δ ADB = Δ ADC (c.g.c)
=>AB = AC
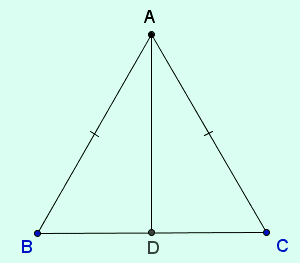
+ Cách 2: chứng minh tam giác đó có 2 góc bằng nhau
Ví dụ: GT Δ ABC cân ở A
Góc BAD = Góc CAD
KL Góc B = Góc C
Chứng minh:
Ta có AB = AC (tam giác ABC cân)
Góc BAD = Góc CAD (gt)
Cạnh AD chung.
Vậy ΔABD = ΔACD (c-g-c)
Suy ra Góc B = Góc C
Kết luận: Tam giác ABC cân có hai góc đáy bằng nhau.
4 . Bài tập áp dụng các cách chứng minh tam giác cân
Bài tập ví dụ số 1: Trong các tam giác ở các hình 15a, b, c, d, tam giác nào là tam giác cân, tam giác nào là tam giác đều ? Vì sao ?
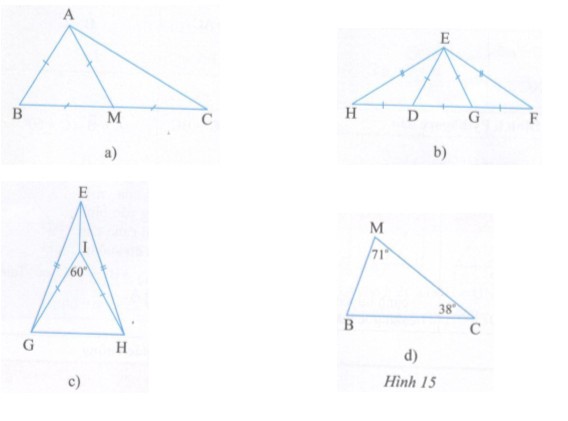
Giải:
a ) Ta có: AB = BM = AM (gt) => tam giác ABM đều.
AM = CM (gt) => tam giác MAC cân tại M.
b ) Ta có: ED = DG = EG (gt) => tam giác EDG đều.
DH = DE => tam giác DEH cân tại D.
Ta có: EG = GF => tam giác GEF cân tại G.
Ta có: EH = EF => tam giác EHF cân tại E.
c) Ta có: IG = IH (gt) => tam giác IGH cân tại I. Mà
Ta có: EG = EH (gt) => tam giác EGH cân tại E.
d ) Tam giác MBC có:
Do đó:
Ta có: Góc B = góc M (=71 o ) =>ΔCBM cân tại C
Bài 2: Cho hình 16, biết ED = EF ; EI là tia phân giác của
Chứng minh rằng :
a)
b) cân.
Giải:
a ) Xét tam giác EID và EIF ta có:
ED = EF (gt)
(EI là tia phân giác của góc DEF)
EI là cạnh chung.
Do đó:
b )
Bài 3: Cho tam giác ABC cân tại A. Tia phân giác của góc B cắt tại F, tia phân giác của góc C cắt AB tại E.
a ) Chứng minh rằng
b ) Chứng minh rằng tam giác AEF cân.
c ) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và IEF là những tam giác cân.
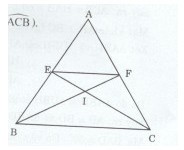
Giải:
Bài 4: Cho tam giác ABC cân tại A, biết góc A = 50o
a ) Tính
b ) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng cân.
c ) Chứng minh rằng MN // BC.
Giải:
